Plano
Alfabeto do Plano:
Existem 7 tipos diferentes de planos caracterizados pela sua posição em relação aos planos de projecção. Estes são:








Alguns destes planos são planos projectantes. Estes planos são perpendiculares (fazem um ângulo de 90º) com pelo menos um dos planos de projecção.
Consegues identificar quais são os planos projectantes?
Estes planos são especiais porque na projecção em que eles são projectanteso seu traço do plano funciona como uma projecção, isto é, nós conseguimos ver o plano todo projectado no próprio traço, então, qualquer recta ou ponto que pertença a esse plano tem que ter a projecção homonima contida no traço do plano.
EXEMPLO Plano projectante frontal
EXEMPLO Plano projectante horizontal
O plano
em dupla projecção ortogonal
Um plano é constituído por um conjunto infinito de rectas e pontos.
2 rectas ; 1 recta e 1 ponto ou 3 pontos
Para definir um plano precisamos de:
Na verdade, precisas sempre de duas rectas - parelelas ou concorrentes - para que o plano esteja definido. Quando o que te é dado são uma recta e um ponto ou três pontos, o teu primeiro objectivo é arranjar forma de transformar o que tens em duas rectas.

duas rectas concorrentes
ou duas rectas paralelas
se for dado uma recta e um ponto, desenha-se, a passar no ponto, uma recta concorrente com a dada ou paralela à dada:


se forem dados 3 pontos, escolhe-se um para ser o ponto de concorrencia e desenham-se duas rectas concorrentes nesse ponto ou faz-se uma recta unindo dois dos pontos e no que ficou de fora, desenha-se uma outra recta paralela a essa.
Importa reter que são necessárias sempre duas rectas para definir um plano. Os traços do plano acham-se unindo os traços de uma das rectas aos traços da outra recta.
No papel, um plano é definido pelos seus traços nos planos de projecção horizontal (hα) e frontal (fα).
Os traços são as rectas que surgem onde o plano "rasga" os planos de projecção e, portanto, os dois traços do mesmo plano encontram-se sempre no x.
Os planos não têm projecções. Só traços.

Rectas contidas em planos
Quando uma recta pertence a um plano, os seus traços (pontos H e F) estão contidos nos traços homonimos do plano (hα e fα)
O ponto comunica com a recta pelas projecções. A recta só comunica com o plano pelos seus traços. Não pelas projecções porque os planos não têm projecções.
Projecções e traços são coisas diferentes e não comunicam (ver em cima "Traços ≠ Projecções").







Recta de topo num plano de topo
Vê aqui o que acontece se os traços da recta não estiverem mesmo em cima dos traços do plano.
Existem algumas rectas que não têm um dos traços e existe a recta fronto-horizontal que não tem traços F nem H. Pensa no espaço quando estiveres a desenhar rectas destas em planos.
Alguns exemplos:
Recta de topo num plano horizontal
Recta fronto-horizontal num plano de rampa
Rectas Notáveis dos planos
Algumas rectas são especiais porque conseguem comunicar com os planos pelas projecções para além dos traços.
Estas são as: Horizontais, Frontais, Recta de maior declive e a de maior inclinação.
Horizontais e frontais
Os traços de uma recta são os pontos que surgem no sitio onde a recta encontra os planos de projecção.
Uma recta esta contida num plano quando os seus traços estão contidos nos traços homónimos do plano.
Este tipo de rectas só têm um dos traços – a recta horizontal só tem traço frontal e a recta frontal só tem traço horizontal.
"Uma recta pertence a um plano quando os seus traços estão contidos nos traços do plano" – Na projecção onde a recta não tem traço, o traço do plano fica paralelo à projecção da recta.
Estas rectas são especiais porque só por si, mesmo se não tivermos os traços do plano, indicam-nos como é que eles estão, qual o ângulo que cada traço faz com o x.
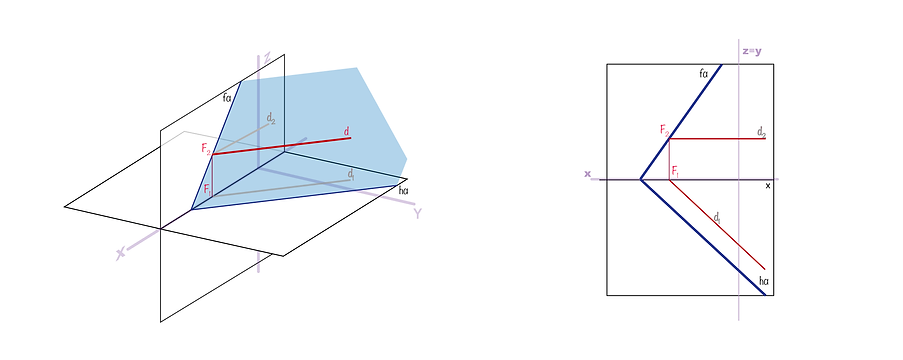

Recta de maior declive
As rectas de maior declive de um plano são perpendiculares ao traço horizontal desse plano. Indica-nos qual é o declive do plano em relação ao PHP.
Em dupla projecção ortogonal, a projecção horizontal desta recta é perpendicular ao traço horizontal do plano.

Recta de maior inclinação
As rectas de maior inclinação são semelhantes às de maior declive mas são perpendiculares ao traço frontal do plano que a contém.
Indica-nos qual é a inclinação do plano em relação ao PFP.
Em dupla projecção ortogonal, a projecção frontal desta recta é perpendicular ao traço frontal do plano.

Pontos contidos em planos
Projecções e traços não comunicam entre eles. Se os pontos só têm projecções e os planos têm apenas traços, então pontos e planos não comunicam em dupla projecção ortogonal. Isto é, em dupla projecção ortogonal, a projecção de um ponto não cai em cima do traço do plano em que está contido (excepto no caso especial dos planos projectantes). As rectas conseguem comunicar com os planos mas não pelas projecções, comunicam pelos traços porque a recta têm projecções e traços. Os traços da recta têm que estar em cima dos traços do plano para que ela pertença ao plano.
Para que um ponto pertença a um plano, este ponto tem que estar contido numa recta que pertença ao plano. Ou seja: As projecções do ponto têm que estar nas projecções de uma recta e os traços da recta têm que estar nos traços do plano. Assim o ponto pertence ao plano.



No caso seguinte, o ponto A não pertence ao plano! Não é directamente em cima dos traços do plano!


Existem duas excepções à regra. formas de um ponto pertencer a um plano tendo as suas projecções, de facto, em cima dos traços dos planos:
Se for o ponto onde o plano cruza o eixo do x;
Se o ponto pertencer a um dos traços do plano - funciona como um traço de uma recta, tem cota ou afastamento nulo.